Unity | 最大公約数、最小公倍数を計算＆Tips

整数の最大公約数、最小公倍数を計算するスクリプトを書きます。

計算を行うスクリプト
1. 最大公約数、最小公倍数を求めるスクリプト
2. テスト用スクリプト
ユークリッドの互除法
1. 最大公約数を求める
2. 最小公倍数を求める
Tipsメモ
1. 名前空間.型の短縮
参考

計算を行うスクリプト

内容は以下の２つです。

呼び出して使用する最大公約数、最小公倍数を求めるスクリプト
確認を行うテスト用スクリプト

最大公約数、最小公倍数を求めるスクリプト

EuclideanAlgorithmクラスのメソッドは以下の２つです。

GCDはm,nの最大公約数を求めます
LCMはm,nの最小公倍数を求めます

using System;
namespace BlueBreath.BBMath
{
    public static class EuclideanAlgorithm
    {
        public static int GCD(int m, int n) => n == 0 ? Math.Abs(m) : GCD(n, m % n);
        public static int LCM(int m, int n) => m == 0 && n == 0  ? 0 :Math.Abs(m * n / GCD(m,n));
    }
}

テスト用スクリプト

確認用のスクリプトです。適当なGameObjectに取り付けて確認します。

using EA = BlueBreath.BBMath.EuclideanAlgorithm;
using UnityEngine;
#if UNITY_EDITOR
using UnityEditor;
#endif
namespace BlueBreath.BBPractice
{
    public class OperationTester : MonoBehaviour
    {
        public void ModTest(){
            Debug.Log("13 % 11 =" + 13 % 11);    //13 % 11 =2
            Debug.Log("13 % -11 =" + 13 % -11);  //13 % -11 =2
            Debug.Log("-13 % 11 =" + -13 % 11);  //-13 % 11 =-2
            Debug.Log("-13 % -11 =" + -13 % -11);//-13 % -11 =-2

            Debug.Log("11 % 13 =" + 11 % 13);    //11 % 13 =11
            Debug.Log("11 % -13 =" + 11 % -13);  //11 % -13 =11
            Debug.Log("-11 % 13 =" + -11 % 13);  //-11 % 13 =-11
            Debug.Log("-11 % -13 =" + -11 % -13);//-11 % -13 =-11
        }
        public int m;
        public int n;
        public void GCDTest() => Debug.Log(m + "と" + n + "の最大公約数は" + EA.GCD(m,n));
        public void LCMTest() => Debug.Log(m + "と" + n + "の最小公倍数は" + EA.LCM(m,n));
    }
    #if UNITY_EDITOR
    [CustomEditor(typeof(OperationTester))]
    public class OperationTesterEditor : Editor
    {
        public override void OnInspectorGUI()
        {
            OperationTester myTarget = (OperationTester)target;
            if(GUILayout.Button("ModTest"))myTarget.ModTest();
            EditorGUILayout.BeginHorizontal();
            myTarget.m = EditorGUILayout.IntField("M:", myTarget.m);
            myTarget.n = EditorGUILayout.IntField("N:", myTarget.n);
            EditorGUILayout.EndHorizontal();
            if(GUILayout.Button("GCDTest"))myTarget.GCDTest();
            if(GUILayout.Button("LCMTest"))myTarget.LCMTest();
        }
    }
    #endif
}

ModTest

ModTestは剰余の計算テストです。

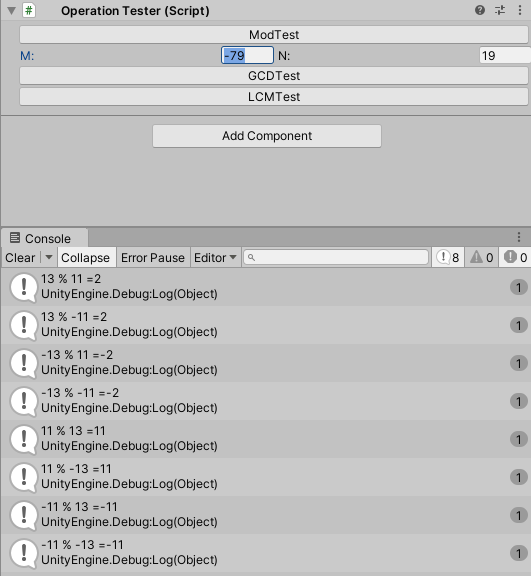
GCDTest

GCDTestはm,nの最大公約数を求めるテストです。

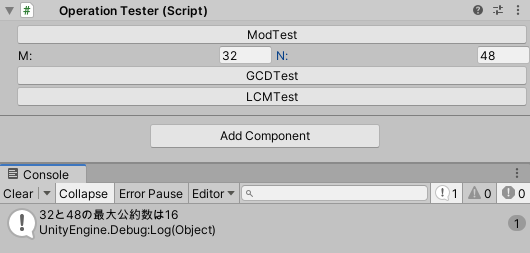
LCMTest

LCMTestはm,nの最小公倍数を求めるテストです。

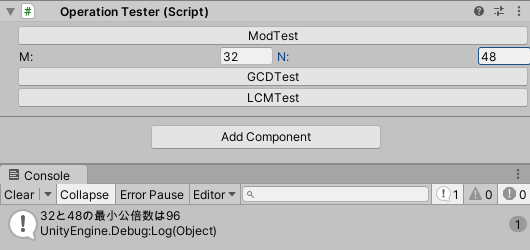
計算はユークリッドの互除法を用いて行いました。

ユークリッドの互除法

ユークリッドの互除法は、二つの自然数の最大公約数を求める手法の一つです。

二つの自然数$m,n(m>=n)$について、$m = nq + r$ の時、m,nの最大公約数はn,rの最大公約数と等しいという性質を利用したものです。

今回はこの手法を用いて最大公約数、最小公倍数を求めます。

最大公約数を求める

２つの整数の最大公約数を求めるためにユークリッドの互除法を用います。

$r = 0$(あまりなし)の場合$m = nq$となり$n$が最大公約数となります。

手続き的に記述すると、次のようになる。
1. 入力を m, n (m ≧ n) とする。
2. n = 0 なら、 m を出力してアルゴリズムを終了する。
3. m を n で割った余りを新たに n とし、更に元のnを新たにm とし 2. に戻る。
ユークリッドの互除法の手続き的記述

この手順を三項条件演算子を用いて記述すると、最大公約数GCDを求める関数は以下の様になります。

public static class EuclideanAlgorithm
{
    public static int GCD(int m,int n) => n == 0 ? Math.Abs(m) : GCD(n, m % n);
}

$n == 0$が真つまりmと0の最大公約数として|m|を返します。

$n == 0$が偽つまり余りが求められる時、GCD(n,m % n)を再帰します。

m,nが整数の範囲の振る舞い

$|m|<|n|$の時m % n = mとなり、$GCD(n,m)$を再帰します。

※補足

m,nが負の値を持つ場合C#上で剰余演算子%の剰余の符号は、左側のオペランドと同じ符号になります。
$n != 0, m==0$の場合GCD(n,0%n) = GCD(n,0) を再帰し|n|を返します
m=nの場合再帰した m % nは必ず0となり|n|(=|m|)を返します。（例　11と11の最大公約数は11）
※3.により、このコードでは、0と0の最大公約数GCD(0,0)は0を返します。

最小公倍数を求める

最小公倍数は公倍数のうち0を含まない最小の値です。２つの正整数m,nに対して、

$$最大公約数*最小公倍数=m*n$$

$$最小公倍数=\frac{m*n}{最大公約数}$$

であり、最小公倍数LCMを求める関数は以下の様になります。

public static class EuclideanAlgorithm
{
    public static int GCD(int m, int n) => n == 0 ? Math.Abs(m) : GCD(n, m % n);
    public static int LCM(int m, int n) => m == 0 && n == 0  ? 0 :Math.Abs(m * n / GCD(m,n));
}

※0と0の最小公倍数は0を除くため存在しませんが、このコードでは、LCM(0,0)は$0*0/0$を計算する事になる為0を返します。

Tipsメモ

名前空間.型の短縮

静的メソッド等を呼び出す際にクラス名が長い場合、名前空間または型のエイリアスを作成して短縮することが出来ます。これはusingエイリアスディレクティブと呼ばれています。

using BlueBreath.BBMath;
// EuclideanAlgorithm.GCD(m,n);
using EA = BlueBreath.BBMath.EuclideanAlgorithm;
// EA.GCD(m,n);

参考

フリー百科事典『ウィキペディア（Wikipedia）』

.NET C# リファレンス

剰余演算子 %